Podstawą wielu algorytmów wykorzystywanych w sztucznej inteligencji jest algebra liniowa. Dlatego bardzo ważne jest poznanie przynajmniej podstaw tej dziedziny matematyki. Najpierw przyjrzyjmy się kilku podstawowym strukturom matematycznym, czyli skalarom, wektorom, macierzom i tensorom. W kolejnych częściach poradnika przejdziemy do operacji matematycznych z wykorzystaniem opisywanych struktur.
Czym jest skalar?
Skalar to liczba, która może przyjmować wartości ujemne lub dodatnie. Dodawanie lub też mnożenie wykonujemy tak jak w przypadku zwykłych liczb. Skalary zapisujemy zazwyczaj kursywą. Przykład definicji skalaru rzeczywistego s: ![]()
Czym jest wektor?
Wektor to nic innego jak tablica liczb, których identyfikacja jest możliwa za pomocą indeksu określającego położenie. Wektory identyfikują punkty w przestrzeni. Załóżmy, że mamy wektor x. Pierwszym elementem tego wektora jest x1, drugim x2, a ostatnim xn, co przedstawiono na poniższym rysunku:

Czym jest macierz?
Macierz to podobnie jak wektor tablica liczb, tyle że dwuwymiarowa. Identyfikacja konkretnej liczby jest możliwa za pomocą dwóch indeksów określającym położenie. Macierze są zapisywane w postaci prostokątnej tablicy i są oznaczane zazwyczaj dużą literą alfabetu, co pokazano na przykładzie poniższej macierzy K:
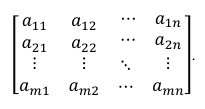
Elementy aji nazywamy elementami macierzy. Przykładowo element a12 znajduje się w pierwszym wierszu i drugiej kolumnie macierzy, bowiem wiersze numerujemy „od góry”, a kolumny – „od lewej strony”. Prezentowana macierz ma wymiary m x n.
Czym jest tensor?
Czasem potrzebujemy tablic o większej liczbie wymiarów. Ogólnie rzecz biorąc liczby tablicy tworzą regularną siatkę ze zmienną liczbą osi, którą nazywamy tensorem. Tensor jest „pojemnikiem” na dane. Możemy mieć tensor 0D, do którego mieści się jeden skalar. Tensor 1D jest nazywany wektorem. Tensor 2D to macierz.
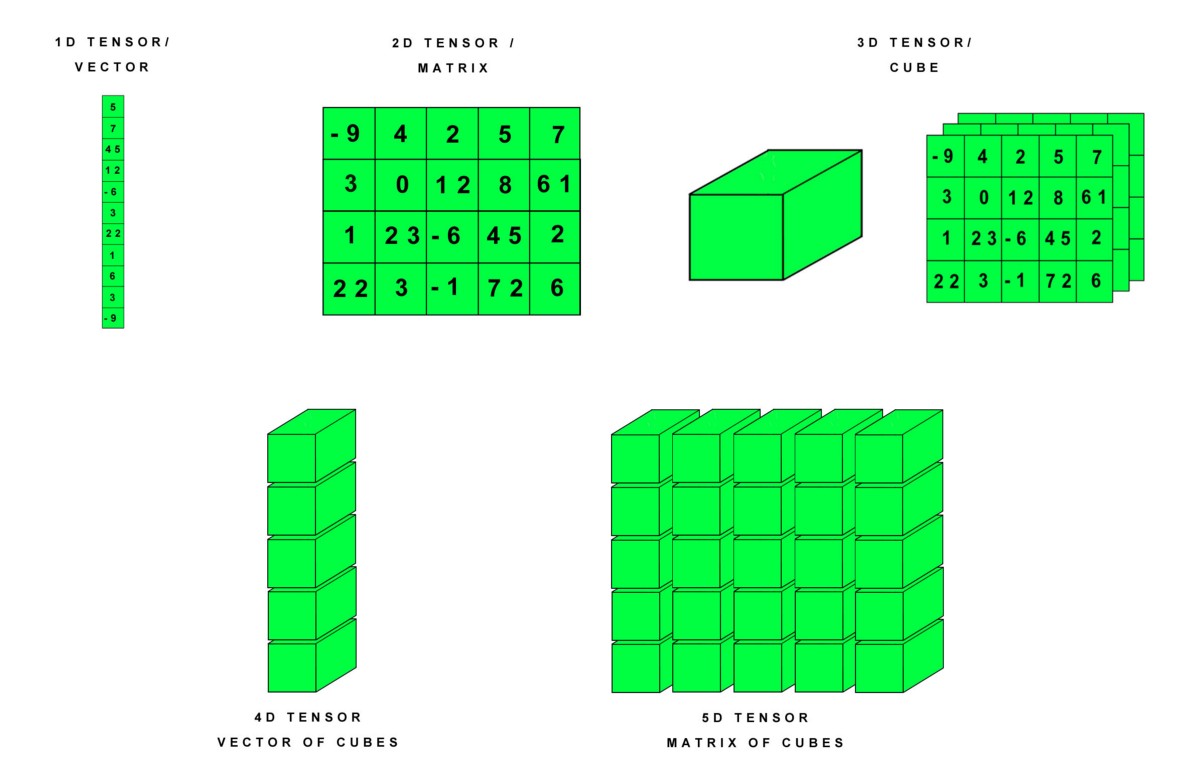
Często potrzebujemy przechowywać wiele tensorów 2D razem. Otrzymujemy wtedy tensor 3D, czyli sześcian liczb. Możemy łączyć owe kostki / sześciany ze sobą, tworząc tensory 4D, 5D,…, ND.
Tensory oznaczamy przy pomocy pogrubionej czcionki i drukowanych liter. Przykładowo element tensora A o współrzędnych (i,j,k) zapisujemy następująco: A i,j,k. W uczeniu maszynowym tensory wykorzystujemy do przechowywania różnych typów danych, np. tensory 3D do szeregów czasowych, 4D do obrazów, a 5D do wideo.